Τα ΕΚΦΕ Σερρών, Πιερίας, Λακωνίας, Λέσβου και 1ο Ηρακλείου, σε συνεργασία πλέον με το Iνστιτούτο Αστρονομίας, Αστροφυσικής, Διαστημικών Εφαρμογών & Τηλεπισκόπησης του Εθνικού Αστεροσκοπείου Αθηνών και με την υποστήριξη του Υπουργείου Παιδείας και της Πανελλήνιας Ένωσης Υπεύθυνων ΕΚΦΕ (ΠΑΝΕΚΦΕ), διοργάνωσαν τη Δευτέρα 20 Μαρτίου 2017 (Εαρινή Ισημερία), δράση με τίτλο «Το Πείραμα του Ερατοσθένη για τον υπολογισμό της ακτίνας της Γης».
Η διαδικασία των παρατηρήσεων, των μετρήσεων και των υπολογισμών υπεισέρχεται στη γνωστική περιοχή αρκετών σχολικών μαθημάτων όπως η Φυσική, η Γεωγραφία, τα Μαθηματικά, η Πληροφορική κλπ.
Στον εμπλουτισμένο χάρτη των «μαθητών του Ερατοσθένη και εραστών της μάθησης», αποτυπώνονται διακριτικά: ο ενθουσιασμός, το πνεύμα συνεργασίας, η φαντασία, η ευρηματικότητα των συμμετεχόντων κι άλλες πολλές αξίες των συμμετεχόντων των 450 και πλέον σχολείων που συμμετείχαν φέτος. (ο χάρτης διαρκώς ανανεώνεται)

Εδώ θα βρείτε το Δελτίο Τύπου
Περισσότερες πληροφορίες και οδηγίες για τη συμμετοχή στη δράση θα βρείτε στην ιστοσελίδα του Αστεροσκοπείου Αθηνών, στη διεύθυνση: http://www.astro.noa.gr/gr/eratosthenes
Ηλεκτρονική διεύθυνση επικοινωνίας με τους συντονιστές της δράσης:

Λίγα λόγια για την ιστορία του πειράματος
Ο Ερατοσθένης (3ος π.Χ. αιώνας) ήταν Διευθυντής της μεγάλης Βιβλιοθήκης της Αλεξάνδρειας, όπου σε έναν πάπυρο διάβασε ότι το μεσημέρι της 21ης Ιουνίου (θερινό ηλιοστάσιο), στα νότια όρια της πόλης Συήνη (Ασσουάν), οι κατακόρυφοι στύλοι δεν ρίχνουν καθόλου σκιά και ο Ήλιος καθρεφτίζεται ακριβώς στον πυθμένα ενός πηγαδιού (δηλαδή, βρίσκεται στο Ζενίθ του τόπου). Ως επιστήμονας, λοιπόν, ο Ερατοσθένης διερωτήθηκε, εάν συμβαίνει το ίδιο ταυτόχρονα και σε μια άλλη πόλη πχ. στην Αλεξάνδρεια. Όμως στην Αλεξάνδρεια, κατά την ίδια μέρα και ώρα, οι κατακόρυφοι στύλοι έριχναν σκιά.
Αν η Γη ήταν επίπεδη, οι κατακόρυφοι στύλοι στις δυο πόλεις θα ήταν παράλληλοι και θα έπρεπε και οι δυο να ρίχνουν σκιά. Αφού, λοιπόν, αυτό δεν είναι αλήθεια, τι μπορεί να συμβαίνει; Την απάντηση έδωσε ο Ερατοσθένης υποστηρίζοντας ότι η επιφάνεια της Γης δεν είναι επίπεδη αλλά σφαιρική. Αυτό το συμπέρασμα είναι, προφανώς, θεμελιώδους σημασίας και επιπλέον επέτρεψε στον Ερατοσθένη να προσδιορίσει την ακτίνα και το μήκος της περιφέρειάς της Γης. Πραγματικά, από το μήκος της σκιάς υπολογίζεται αμέσως η διαφορά των γεωγραφικών πλατών των δύο πόλεων, ίση περίπου με 7 μοίρες. Επειδή η απόσταση των δύο πόλεων ήταν γνωστή από αφηγήσεις βηματιστών και ίση περίπου με 800 Km (φημολογείται ότι ο Ερατοσθένης μίσθωσε βηματιστές για τη μέτρησή της), η περιφέρεια της Γης υπολογίστηκε ίση με 40000 Km.
Αυτή είναι η σωστή απάντηση και ο Ερατοσθένης την έδωσε χρησιμοποιώντας ως μόνα εργαλεία ράβδους, μάτια, πόδια, μυαλό με απλότητα σκέψης και επινοητικότητα. Το λάθος στον υπολογισμό ήταν μόνο 2%, ένα πραγματικά αξιοσημείωτο επίτευγμα για περίπου πριν από 2,5 χιλιετίες. Άρα, ο Ερατοσθένης ήταν ο πρώτος άνθρωπος που μέτρησε τις διαστάσεις του πλανήτη Γη, γι' αυτό και θεωρείται δημιουργός της μαθηματικής γεωγραφίας.

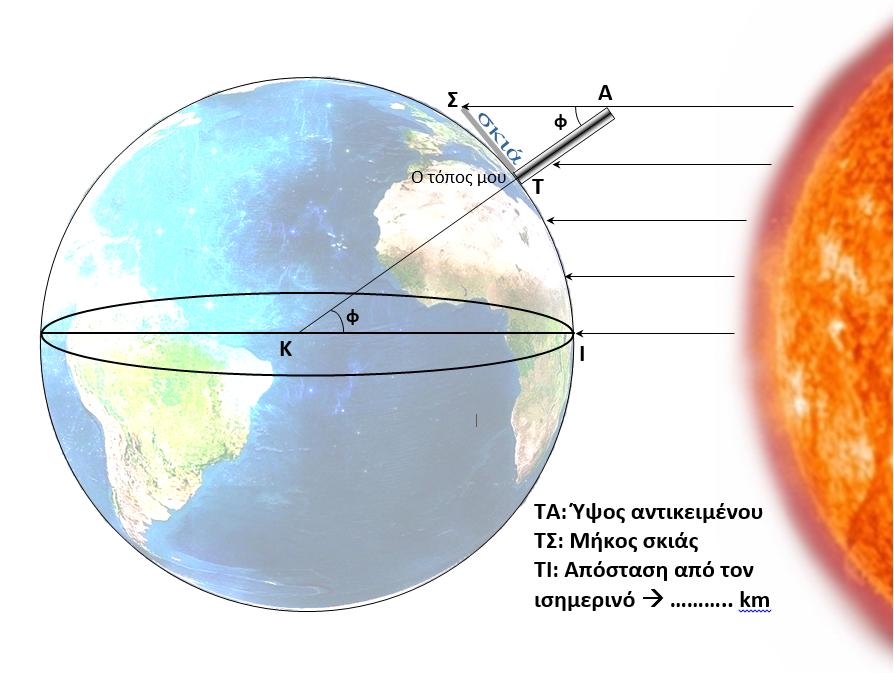
Αν θεωρήσουμε ότι ο κύκλος στο διπλανό σχήμα είναι η Γη τότε η έλλειψη στο κέντρο είναι ο ισημερινός. Στον ισημερινό αυτές τις μέρες ο Ήλιος το μεσημέρι βρίσκεται στο ζενίθ. Επομένως οι ακτίνες πέφτουν κατακόρυφα και ο Ήλιος καθρεφτίζεται στον πυθμένα ενός πηγαδιού. Η προέκταση μιας ακτίνας του είναι η ΙΚ και περνάει από το κέντρο της Γης Κ.
Έστω ότι εμείς είμαστε στη θέση Τ. Αν τοποθετήσουμε μια κατακόρυφη ράβδο ΤΑ=Υcm τότε αυτή το μεσημέρι (στις 12:34 μ.μ. για τις Σέρρες) έχει σκιά ΤΣ=Χcm.
Σημ. Βρείτε εδώ την ώρα που πρέπει να κάνετε τη μέτρηση σε κάθε τόπο
Υπολογίζουμε την εφαπτομένη της γωνίας ΣΑΤ από το λόγο Χ/Y και έτσι βρίσκουμε την γωνία που είναι φ μοίρες. Η γωνία φ είναι ίση με την επίκεντρη γωνία ΤΚΙ. Το γεωγραφικό πλάτος της θέσης μας είναι φ μοίρες.
Παρατήρηση: Η γωνία φ είναι ίση με το γεωγραφικό πλάτος μόνο αν η μέτρηση γίνει τις μέρες της εαρινής ή φθινοπωρινής ισημερίας.
Από το google earth ή από εδώ βρίσκουμε την απόσταση ΤΙ=S. Είναι η απόσταση της θέσης μας από τον Ισημερινό. Με μια απλή αναλογία υπολογίζουμε την περίμετρο της Γης και μετά την ακτίνα της R.      

Μια εισήγηση του Μανδηλιώτη Σωτήρη, υπεύθυνου του ΕΚΦΕ Σερρών με τίτλο "Ερατοσθένης ο Κυρηναίος ή Πένταθλος", η οποία πραγματοποιήθηκε στο πλαίσιο της επιμορφωτική ημερίδας με θέμα «Από την Αρχαία Ελληνική Φιλοσοφία στη σύγχρονη Επιστημολογία» που συνδιοργάνωσαν οι Σχολικοί Σύμβουλοι Φιλολόγων και Φυσικών Επιστημών, μπορείτε να δείτε εδώ 

Παραδείγματα Παρατήρησης
Στις φωτογραφίες παρατίθενται διάφοροι τρόποι που εφαρμόστηκαν για την μέτρηση της σκιάς ράβδου από το 2010 μέχρι το 2015. Χρησιμοποιήθηκαν βιβλία με χοντρά εξώφυλλα, δοκάρια από εστία, τρίποδας στήριξης οθόνης, ορθοστάτες οργάνων εργαστηρίου, σκουπόξυλα, μέτρο, χαρτόκουτα, γωνιομετρικός δίσκος κ.α.